Показано, что результаты, полученные в рамках разработанного хемоинформационного математического формализма, соответствуют решение одноэлектронного уравнения Шрёдингера на молекулярных фрагментах, аддитивной схеме расчета электронной плотности в теории функционала плотности, а также к поправке интегралов перекрытия в теории молекулярных орбиталей. Алгоритмы, основанные на разработанном формализме, были протестированы на выборке 134 тысячи молекул, для которых вычислены наибольшая энергия занятых молекулярных орбиталей (ВЗМО) и наименьшая незанятая энергия молекулярной орбитали (НСМО), энергия запрещенной зоны ВЗМО-НСМО, константы вращения и т. д. (метод квантово-механических расчетов B3LYP/6-31G(2df,p)). Кросс-валидационное тестирование линейных и нелинейных моделей привело к установлению ранговых корреляций между расчетными и экспериментальными данными в диапазоне r=0,67–0,85. Скорость расчетов по разработанным алгоритмам выше, чем для квантово-механических расчетов, на восемь порядков. Разработанные алгоритмы могут быть использованы для масштабных скринингов молекул при решении задач молекулярной фармакологии и материаловедения.
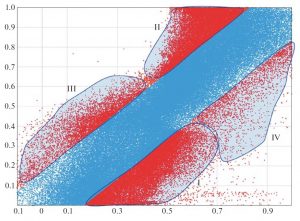
Анализ ошибок расчетов зазора НСМО–ВЗМО (усл. ед.) с областями наиболее типичных ошибок. Полоса на рисунке центр соответствует стандартному отклонению.
Torshin IYu, Rudakov KV. Topological Chemograph Analysis Theory As a Promising Approach to Simulation Modeling of Quantum-Mechanical Properties of Molecules. Part II: Quantum-Chemical Interpretations of Chemograph Theory. Pattern Recognition and Image Analysis, 2022, Vol. 32, No. 1, pp. 205–217. DOI: 10.1134/S1054661821040258 Ссылка на сайт Springer Nature